In the Anoma report we touched on Narwhal a bit because we needed to understand Narwhal to understand Anoma’s Heterogeneous Narwhal. We did not give a full explainer on Narwhal, however, as it was not created by Anoma and somewhat out of scope for the Chimera Chain section. Here, I will explain Narwhal in full (note that there are some Typhon references as this is from an earlier draft that didn’t make the final cut).
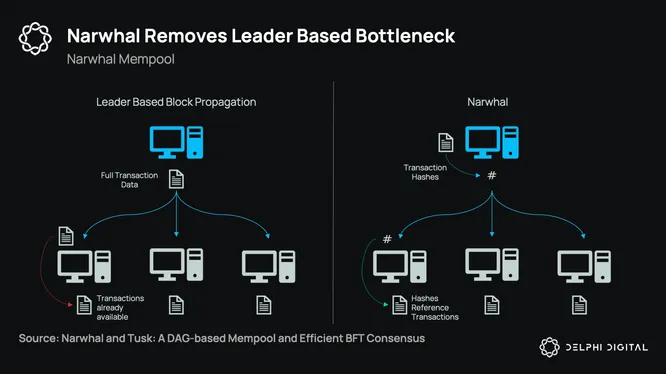
In Narwhal, instead of the proposing validator sending all transactions in a block to the other validators they just send references to transactions that we know are available (that other validators have already received in their local mempools). The transaction data can thus bypass the consensus process, removing the large data transmission step from it. This propagation of data is often the limiting factor/bottleneck in consensus. The more validators you have, the longer it takes to propagate data to all of them and get 2/3 to commit to a block. In essence, instead of being tied together, the mempool (availability) and ordering (consensus) are decoupled. You isolate the data propagation to the mempool and then just reach consensus on metadata, and reaching consensus on metadata is cheap. Consensus gets rid of the “baggage” that is transaction data which just skips consensus and goes straight to the execution engine.
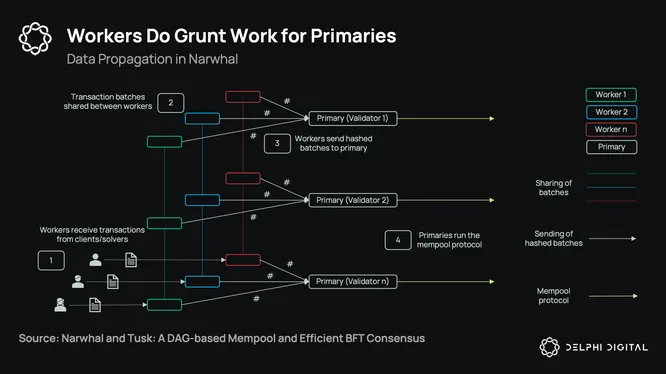
To enable this, Narwhal adds the concepts of “workers” and “primaries”. A single validator will run multiple workers on separate instances (hardware) and a single primary. The workers are responsible for receiving transactions from clients/solvers and then sharing transaction batches to workers of other validators. Notably, each worker receives different transactions and shares the transaction batches with the same workers of other validators. Transactions here are solved batches of intents.
To illustrate: Each validator will have a “worker 1” which shares transaction data between each other validators’ “worker 1”, “worker 2” that shares transaction data between other “worker 2’s”, and so on. We are parallelizing the propagation of transaction data here by having each worker on each validator responsible for a different set of transactions. If a validator also runs their own solver, then they can just send the completed transaction batch to their own worker locally before propagating it to others. Then, each validator’s workers send hashed batches to their primaries, again benefitting from parallelization. The primaries then run the ‘mempool protocol’ with the hashed batches which is lightweight and only works with metadata (blockheaders and hashes). The bulk of the data propagation can thus be pushed to the workers and primaries can work with much lighter data, broadcasting this lighter data to all other primaries to build blocks. This part is what solves the leader bottleneck problem.
This brings us to what are essentially four distinct layers:
-
Ephemeral Mempool: This is where intents are sent/discovered and in transit. Some validators may be aware of some and others not. Solvers compete to complete batches.
-
Logged Mempool: The second layer where batched transaction data is broadcast to everyone for availability.
-
Partial/Pre-Ordering: The transactions (through the primary) are pre-ordered through a DAG.
-
Consensus: Consensus finalizes blocks.
The layer to focus on here is the partial ordering step (#3) as this is where Narwhal’s DAG structure is fundamentally different than others, allowing blocks and their transactions to be ordered through a DAG before being finalized by consensus.
In the example below we start from the perspective of the green validator. The green validator broadcasts their block to all other validators. We need to know that enough of the other validators have received and will store and make available the block as long as needed. The other validators do this by signing the green block (hashes of batches of transactions) and send back the signed data to the green validator. When a full quorum is reached we receive a certificate of availability and integrity for the block. The green validator then sends this certificate to all of the other validators to reference in their future blocks.
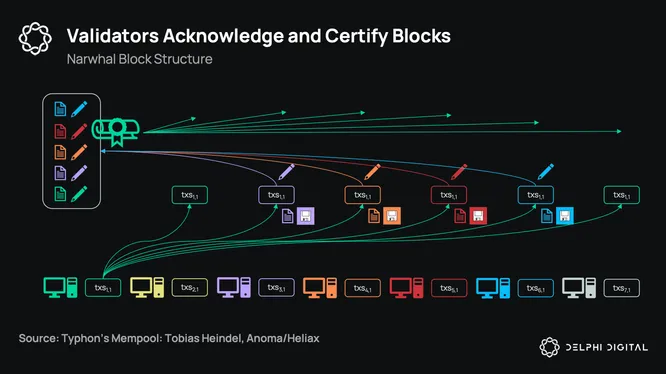
In the genesis round, the green block will be finalized by consensus. Other validators then do the same, broadcasting their own blocks and receiving back certificates of availability in the process. New blocks reference previous certificates of availability from past blocks (and the genesis) and continue to build on top. Notably, these blocks continue to get built in the DAG without involving consensus. Every once and awhile, consensus will run to vote on and finalize a block in the DAG and in the process finalize all previously referenced blocks with certificates of availability.
To illustrate: in the chart below the green “GEN” is the genesis block. New blocks are then built by all validators with their own certificates labelled “X2”, referencing the Genesis certificate. A round of consensus is then run again which commits the red block “2”. All of the “X2” blocks referenced by red block “2” then get committed and ordered. Then another round “3” runs later, again committing new blocks (X3) with referenced certificates. This is how we decouple the building and partial/pre-ordering of the DAG of transaction data from finalizing the total order through consensus.

This is Narwhal. Now you know.